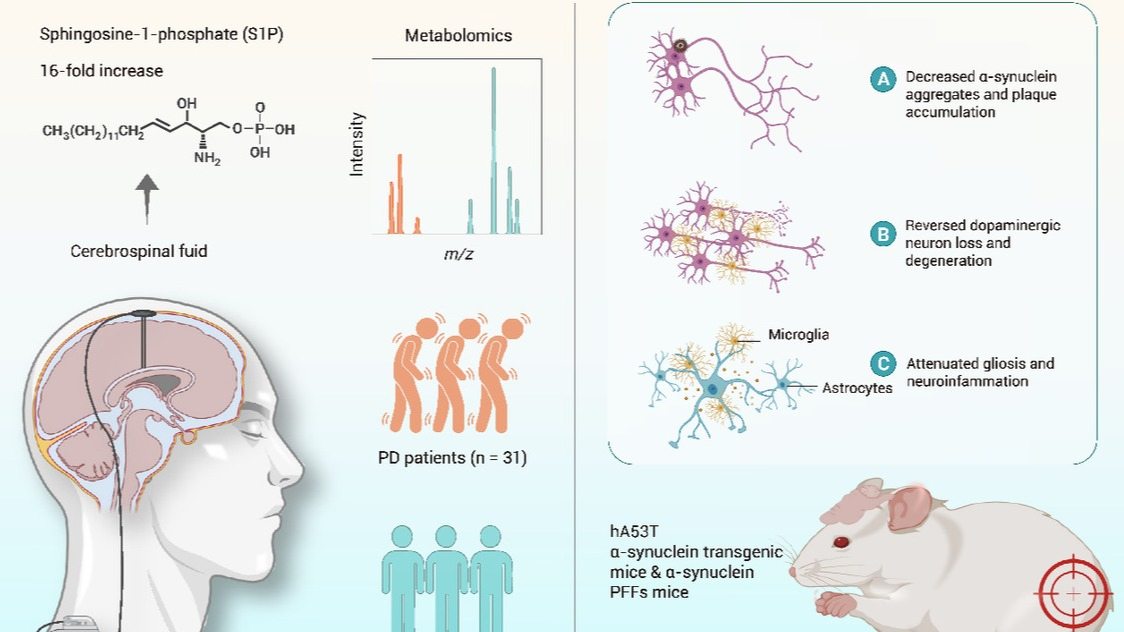
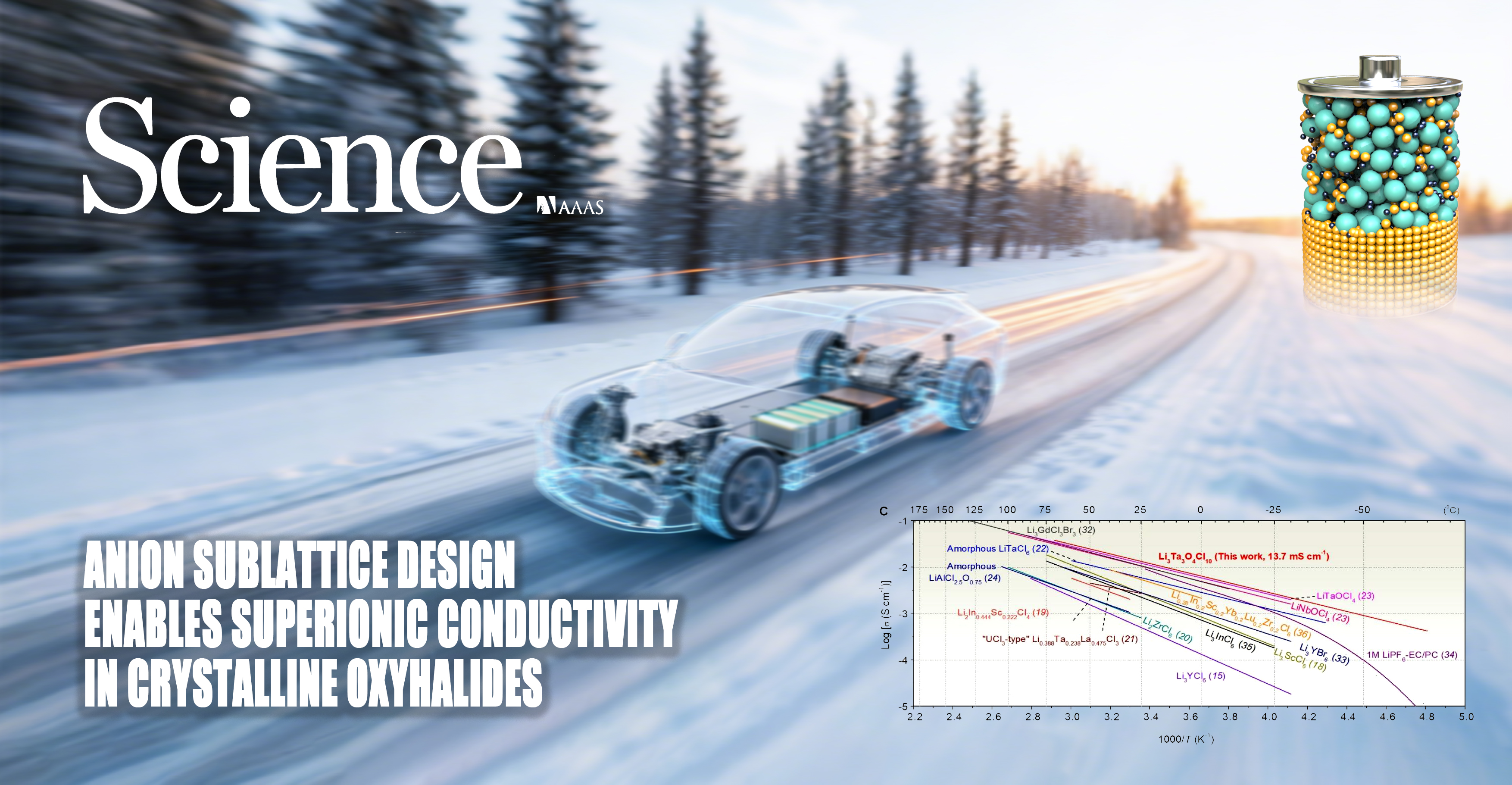
Recently, Associate Professor Zijin Huang from the School of Electronic Science and Technology, College of Information Science and Technology, in collaboration with Assistant Professor Kosmas L. Tsakmakidis from the National and Kapodistrian University of Athens and other collaborators, published a review article titled Topological Rainbow Trapping in the journal Nature Reviews Physics. This article systematically introduces a novel wave-manipulation mechanism – Topological Rainbow Trapping. This mechanism integrates concepts from topological physics and slow-light engineering, thereby enabling robust and frequency-selective wave localization across diverse physical systems.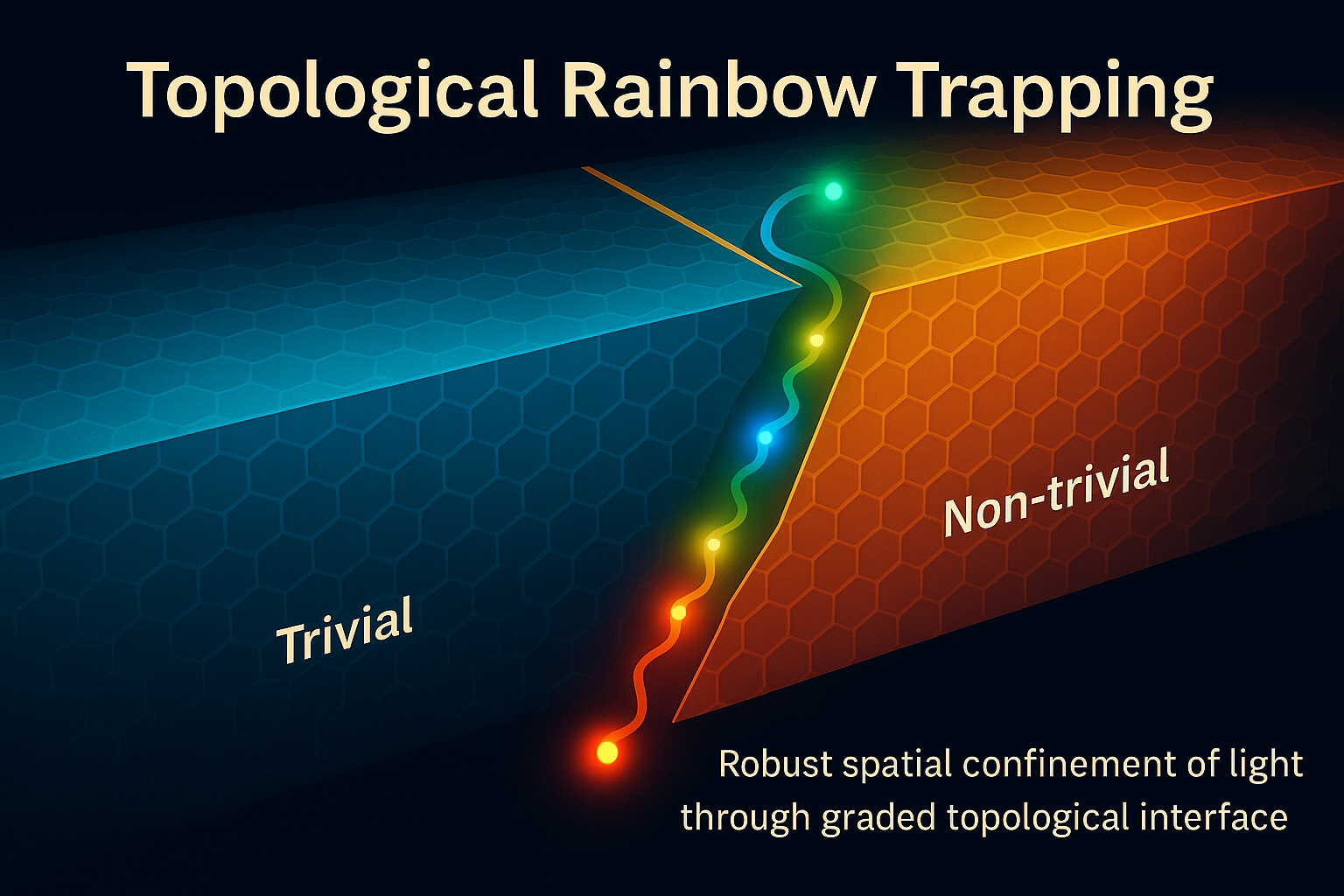
Topological rainbow trapping allows different frequency components of a wave to slow down and separate in space, forming a rainbow-like localized distribution. Conventional rainbow trapping mechanisms, which rely on refractive index gradients, are highly sensitive to fabrication imperfections. In contrast, topological rainbow trapping, benefiting from topological protection, maintains stable wave localization even in the presence of structural defects, energy dissipation, or impurities. This fundamentally enhances the robustness and functionality of slow-light devices.
In this review, the authors delve into the roles of Berry curvature, topological invariants (such as Chern numbers), and synthetic dimensions, demonstrating how they can reshape group velocity and achieve precise, frequency-selective wave localization. The article provides the first clear distinction between two categories of topological rainbow trapping mechanisms: those driven by external gradients and those arising from the intrinsic design of topological band structures. Topological rainbow trapping is presented as a universal, scalable, and defect-robust framework for wave manipulation, applicable to photonic, phononic, and elastic systems.
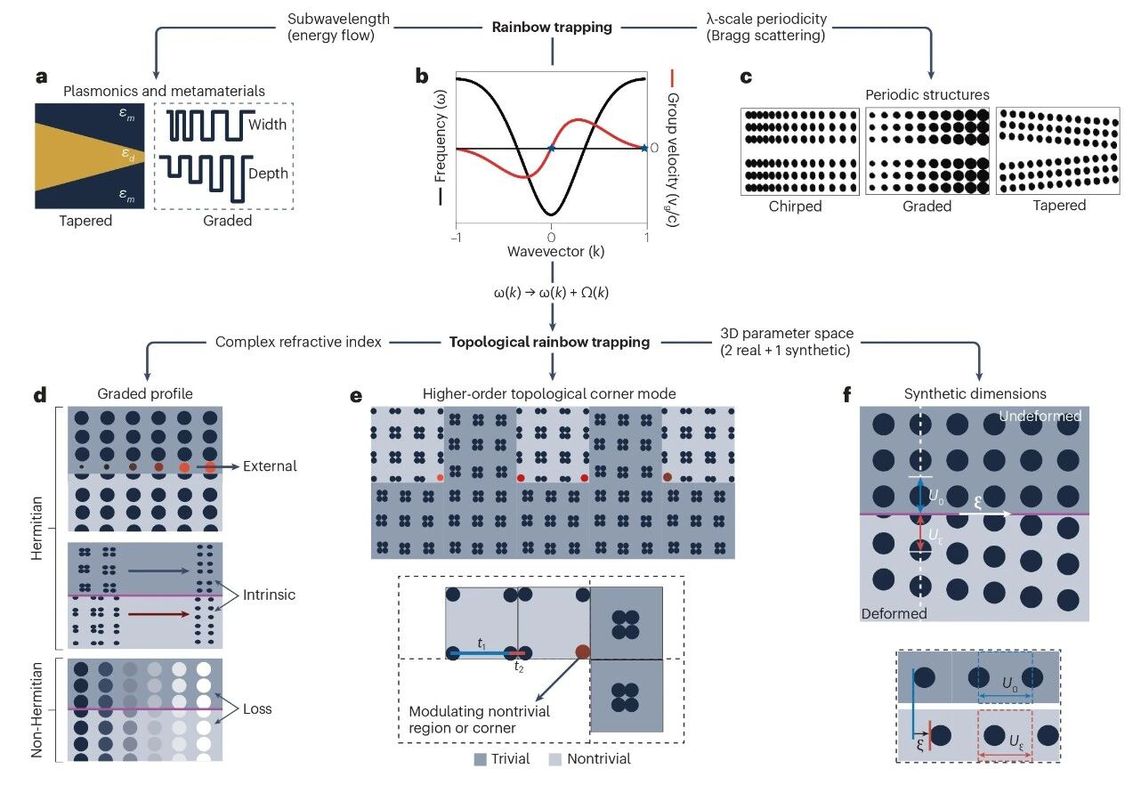
Figure 1. From conventional rainbow trapping to topological rainbow trapping.
Furthermore, the authors systematically categorize the underlying physical principles of topological rainbow trapping into three main mechanisms:
1. Gradient-index driven trapping: This mechanism utilizes spatially varying material parameters to create points of zero group velocity, effectively slowing waves of different frequencies and localizing them at distinct spatial positions.
2. Higher-order topological corner states: This mechanism emerges in specially designed photonic or elastic lattices, facilitating deeply localized corner-bound states that exhibit high immunity to disorder and boundary defects.
3. Synthetic dimension-based trapping: This approach extends the effective dimensionality of the system through frequency or time modulation, enabling wave localization in non-spatial degrees of freedom (see Fig. 1).
The review also addresses several practical challenges in realizing topological rainbow trapping, including energy loss, dynamic tunability, and device miniaturization. Innovatively, it discusses the concept of complex-frequency excitations, a mechanism that enables the system to achieve quasi-stable wave localization by temporarily circumventing energy dissipation (see Fig. 2). The authors also highlight the significant potential of non-Hermitian symmetry breaking, inverse design methods, and AI-assisted optimization for enhancing the performance of devices based on topological rainbow trapping.
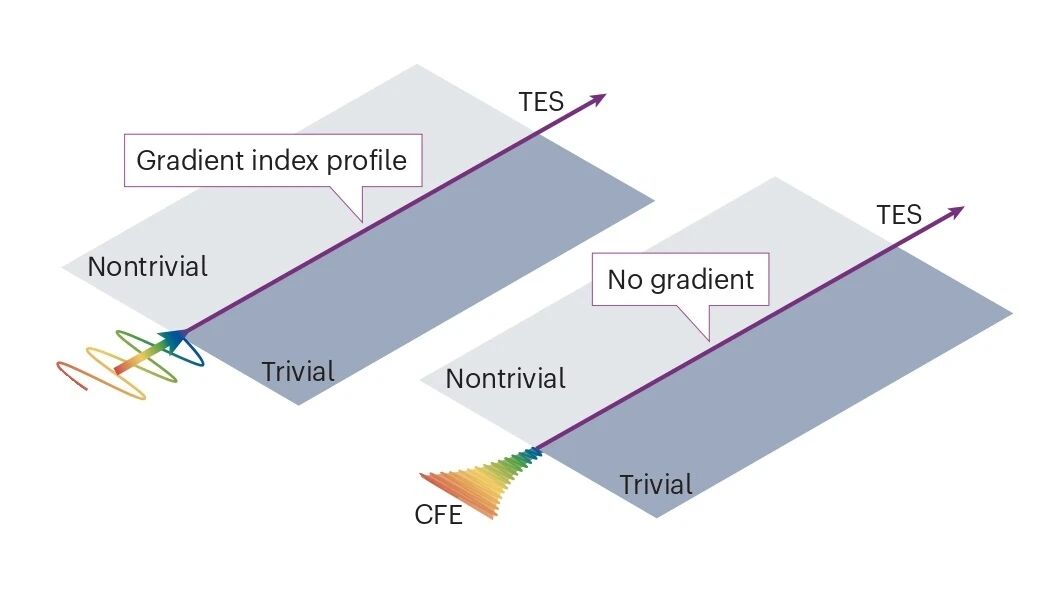
Figure 2. Robust wave localization achieved via complex-frequency excitations.
Topological rainbow trapping is positioned not only as a fundamental concept in wave physics but also as a versatile platform for next-generation photonic and phononic applications. Potential applications include on-chip multiplexing and filtering, quantum light-matter interfaces, nonlinear wave manipulation, and subwavelength energy harvesting in plasmonic systems. The theoretical framework is equally applicable to optical, acoustic, elastic, and non-Hermitian media, underscoring its universality and broad applicability across disciplines.
This article represents a significant advancement in the fields of topological photonics and wave manipulation, providing a unified theoretical foundation, a clear mechanistic classification, and actionable design strategies. It is poised to become an essential reference for researchers seeking to deepen their understanding of the physics and expand application scenarios involving highly robust and multi-frequency wave control.
Research Assistant Professor Sayed El. Soliman of Eastern Institute of Technology, Ningbo is the first author, and Dr. Maria Barlou of the National and Kapodistrian University of Athens is the second author. Associate Professor Zijin Huang of Eastern Institute of Technology, Ningbo and Assistant Professor Kosmas L. Tsakmakidis of the National and Kapodistrian University of Athens are the co-corresponding authors.